Using convolutional networks for object comparison

Recently Google open-sourced their flow graph based numerical computation library Tensorflow. In their words:

TensorFlow was originally developed by researchers and engineers working on the Google Brain Team within Google’s Machine Intelligence research organization for the purposes of conducting machine learning and deep neural networks research, but the system is general enough to be applicable in a wide variety of other domains as well.

In order to learn a little about convolutional networks and how to use Tensorflow, I decided on a little experiment. Could I teach a network to look at two images and tell me if they represented the same object or not? You could do this using single image classifiers. As an example, for MNIST images of handwritten digits 0 to 9, you could just learn a classifier for each digit 0 to 9, classify each image and compare classifications of the two images. To make things a little harder for myself, I wanted to see if the network could learn a more abstract version of discrimination. I wanted to know if I could train a network to do this for pairs of objects where at least one of the objects was unknown to the network. In other words, at least one of the images in the pair represented an object that was not presented to the network at training time.

Tensorflow comes with tutorials and source code used in those tutorials. The Deep MNIST for expert tutorial leads the reader through the steps of creating a relatively simple convolutional network with close to state of the art performance for classifying MNIST digits. I based my network on the network the tutorial created, with some small changes.

Figure: Layers in my network

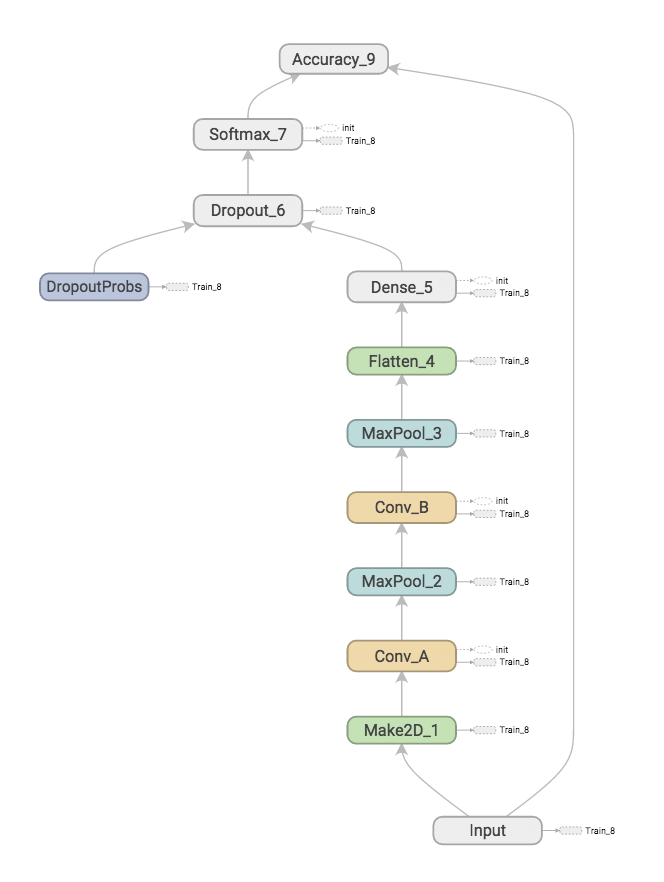
Mainly, instead of presenting the network with 28 x 28 images and a label in \(\{0,1, \ldots, 9\}\), I presented the network with 56 x 28 images created from pairs of 28 x 28 images by stacking them on top of each other. Each of these 56 x 28 images I categorized into

• discordant: the two stacked images were of different digits, and
• concordant: the two stacked images were of the same digits.

Discordant images received a label 0, and concordant ones received a label 1.

The MNIST dataset comes pre-split into test and training sets, of sizes 60,000 and 10,000, respectively. I created my own test and learning sets based on these by randomly sampling pairs of from these such that

• my learning and test sets only contained images from their respective original counterparts,
• each set was roughly the same size of their original counterpart
• each set contained about 50% concordant images

I further divided my learning set into two parts

• training, and
• holdout (approximately 5000 images)

Now, to address my question regarding discerning unseen objects, I made sure that the training set contained only images of digits \(< 7\), so that in testing, I would be testing on pairs where one or more digits were from unseen digits.

I now trained the network on the training set, presenting it with a minibatch of size 50 each round. I also computed the accuracy on the holdout set each 100 rounds, and stopped the training process once the holdout accuracy had not improved in 10 evaluations. This happened after 8500 rounds.

Here are the results on the test set in accuracy numbers:

both > 6   : 0.61659437418
one is > 6 : 0.837075948715
both < 7   : 0.980786502361
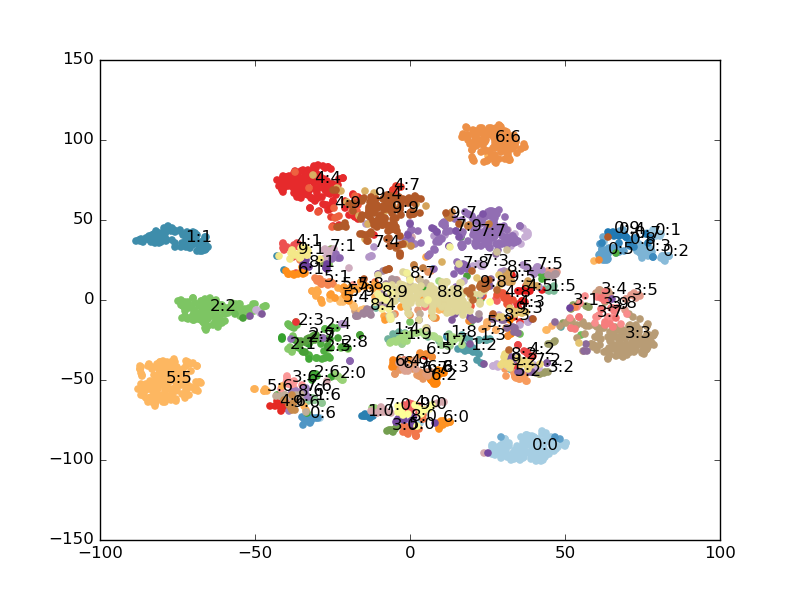
overall    : 0.878497779369

In order to create some visualizations I used t-Distributed Stochastic Neighbor Embedding to cluster the output of the “Dense_5” layer for 2500 randomly chosen test set images in the figure above into two dimensions. I annotated the “center” point of each cluster with ‘x:y,’ where x and y are the original image labels. A plot can be seen here:

Figure: Test pair clusters

Next I randomly chose 9 images from the test set, and systematically occluded 8 x 8 pixel patches and recorded the influence this had on the predicted probability of the correct class (0 or 1). I did this in the hope that this would let me identify portions of the image that were significant for the classification. The results are plotted as heatmaps next to the image here:

Figure: Occlusion test on 9 images

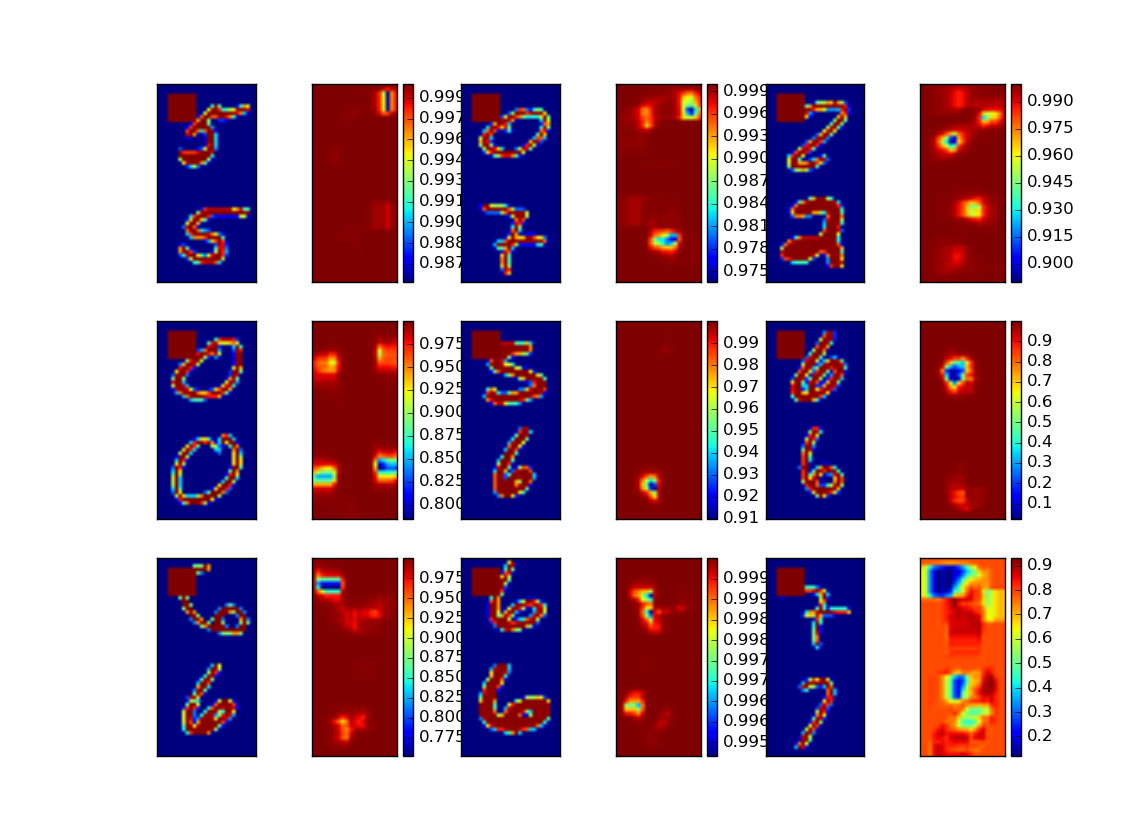
Looking at the results and plots we note the following:

1. classification accuracy is ok when both stacked images are < 7, and seemingly not all that convincing otherwise. However, it is hard to tell from this one experiment.
2. even ‘7:7,’ ‘8:8,’ and ‘9:9’ are recognizable as clusters, even though the network was oblivious to these digits.

An unsupervised challenge is trying to recognize the writers of the MNIST digits. Assuming that the writers, i.e., the people who actually wrote the digits subsequently photographed, contributed more than one image, can we figure out if two images were written by the same writer? This challenge I will leave for another time…